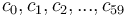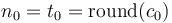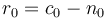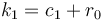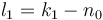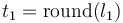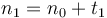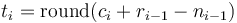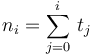Count Rate Compression
Contents
[hide]Solar orbiter data compression proposal
Lets assume we need to transfer a stream of count rates, e.g., a counter read with 1 second resolution, packaged up for a minute.
Rounding Errors
We encode the first count 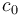 , according to the
compression methode below, which yields a code that represents the
number
, according to the
compression methode below, which yields a code that represents the
number 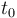 , rounded from
, rounded from 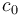 .
.
Where
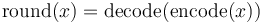 .
The rounding error is within the Poisson statistics of
the count:
.
The rounding error is within the Poisson statistics of
the count:
We add the rounding error to the next count:
Running Difference
And since consecutive counts should be similar, we calculate the differnce between the next counts to what we transfered as the last count, which should compress much better, most of the time:
This will be encoded and sent in telemetry, representing the number
The represented count rate is then
et cetera.
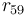 is encoded and appended to the encoded stream.
is encoded and appended to the encoded stream.
To avoid oscillations and bring more regularity into the sequence at
low count rates, the difference is only computed when
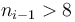 , else, we just encode
, else, we just encode 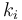 .
.
, if
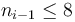
Encoding
The encoding assumes that most numbers are small. There will be lots of zeros. We cut out the Poisson noise, i.e, the dash-bits are not transmitted, only the x-bits. The decoder will add an implicit 1 for the first dash. We need a sign bit.
l r e ------------------------------------------------------------- 0 ±0 0 0/1 1-15 ±0 1s0xxxx 4/7 16-31 ±1 1s10xxx- 5/7 32-63 ±2 1s1100xxx-- 6/9 64-127 ±4 1s1101xxx--- 7/9 128-255 ±4 1s11100xxxx--- 8/11 256-511 ±8 1s11101xxxx---- 9/11 512-1023 ±8 1s111100xxxxx---- 10/13 1024-2047 ±16 1s111101xxxxx----- 11/13 2048-4095 ±16 1s1111100xxxxxx----- 12/15 4096-8191 ±32 1s1111101xxxxxx------ 13/15 8192-16383 ±32 1s11111100xxxxxxx------ 14/17 16384-32767 ±64 1s11111101xxxxxxx------- 15/17 32768-65535 ±64 1s111111100xxxxxxxx------- 16/19 65536-131071 ±128 1s111111101xxxxxxxx-------- 17/19
l t r
--------------
...
14 => 14 0
15 => 15 0
16 => 17 -1
17 => 17 0
18 => 19 -1
19 => 19 0
...
30 => 31 -1
31 => 31 0
32 => 34 -2
33 => 34 -1
34 => 34 0
35 => 34 1
36 => 38 -2
37 => 38 -1
...
With this kind of compression we may gain an order of magnitude data.
Dropping more bits
We can drop even more bits from the stream. Numbers between -3 and 3 could be sent as zero, because so small counts cannot represent high time resolution data, and the counts the we miss will in the end appear in the minute sum.
The first count 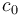 and the last residual
and the last residual
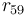 will be sent in full poisson resolution according
to the table above, but the running differences can as well drop one,
two or even three bits.
will be sent in full poisson resolution according
to the table above, but the running differences can as well drop one,
two or even three bits.
E.g., droping 3 bits:
l r e ------------------------------------------------------------- 0-3 ±0 0 2/1 4-15 ±0 1s0x--- 4/4 16-31 ±1 1s10---- 5/4 32-63 ±2 1s1100----- 6/6 64-127 ±4 1s1101------ 7/6 128-255 ±4 1s11100x------ 8/8 256-511 ±8 1s11101x------- 9/8 512-1023 ±8 1s111100xx------- 10/10 1024-2047 ±16 1s111101xx-------- 11/10 2048-4095 ±16 1s1111100xxx-------- 12/12 4096-8191 ±32 1s1111101xxx--------- 13/12 8192-16383 ±32 1s11111100xxxx--------- 14/14 16384-32767 ±64 1s11111101xxxx---------- 15/14 32768-65535 ±64 1s111111100xxxxx---------- 16/16 65536-131071 ±128 1s111111101xxxxx----------- 17/16
Reference Implementation
This is old, ...
#! /usr/bin/python
# -*- coding: utf-8 -*-
import numpy
class bits:
def __init__(self, b=0, e=0):
self.len = b
if b:
self.bits = [(b,e)]
else:
self.bits = []
def __len__(self):
return self.len
def __iter__(self):
return self
def next(self):
try:
return self.pop()
except IndexError:
raise StopIteration
def pop(self, n=1):
b,e = self.bits[0]
while n>b:
bb,ee = self.bits[1]
b += bb
e <<= bb
e |= ee & ((1<<bb)-1)
self.bits[0:2] = [(b-n,e)]
self.len -= n
b -= n
self.bits[0] = (b,e)
return (e >> b) & ((1<<n)-1)
def __add__(self, other):
b = bits()
b.bits = self.bits+other.bits
b.len = self.len+other.len
return b
def copy(self):
b = bits()
b.bits = [t for t in self.bits]
b.len = self.len
return b
def __str__(self):
return "".join([str(b) for b in self.copy()])
def encode(c, drop=0):
if c<0:
m = 0x60
c = -c
else:
m = 0x40
if not ((2*c)>>drop):
return bits(1,0)
b = 7
if c<16:
m |= c
elif c<32:
m |= (c>>1)&7 | 0x10
else:
b = 9
n = 16
m = (m|0x18)<<2
c >>= 2
while c>=n:
c >>= 1
if c<n:
m |= c
break
m = (m|n)<<2
n <<= 1
b += 2
m = m | c&~(n>>1)
return bits(b-drop, m>>drop)
def decode(bb, drop=0):
b = bb.pop()
try:
if b:
s = bb.pop()
n = 0
while b:
b = bb.pop()
n += 1
if not n:
return 0
if n==1:
m = bb.pop(4-drop)<<drop
if drop:
m |= 1 << (drop-1)
if not m:
return None
elif n==2:
m = (bb.pop(3-drop)<<(1+drop)) + 16 + (1<<drop)
else:
b = bb.pop()
m = bb.pop(n-drop)<<drop
m += 1<<n
m = ((m<<1) + (1<<drop)) << (n-2+b)
return m if not s else -m
except IndexError:
raise ValueError
class decoder:
def __init__(self, bb):
self.bb = bb
def __iter__(self):
return self
def next(self):
try:
return decode(self.bb)
except IndexError:
raise StopIteration
def encode_stream(s):
bb = bits()
nn = 0
rr = 0
for c in s:
be = encode(c+rr-nn)
bb += be
t = decode(be)
nn += t
rr += c-nn
return bb+encode(rr)+bits(7,0x40)
def decode_stream(bb):
return [i for i in decoder(bb)]